08. (Optional) Margin Error Calculation
(Optional) Margin Error Calculation
In this optional section, we'll calculate the distance between the two margins in the SVM.
First, recall the notation, where Where W = (w_1, w_2) and x = (x_1,x_2), and Wx = w_1x_1 + w_2x_2.
Notice that all we have three lines, of the following equations:
- Wx+b=1
- Wx+b=0
- Wx+b=-1
And in order to find the distance between the first and the third, we only need to find the distance between the first two, and multiply by two, as these are three equidistant parallel lines. That is, we need to find the distance between the two lines in Figure 1.
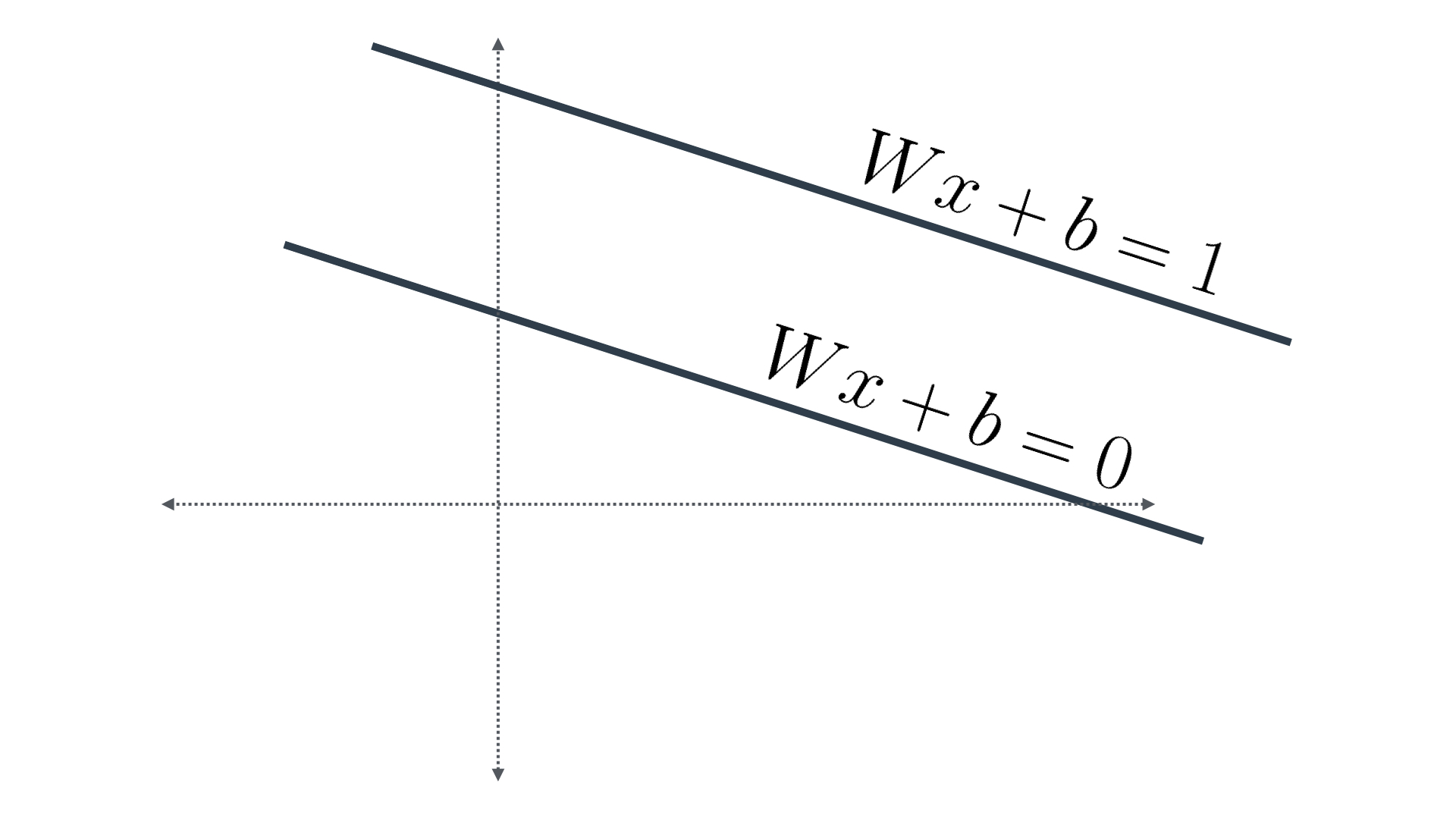
Figure 1
Now, notice that since we're only measuring distances between lines, we might as well translate these two lines, so that one of them touches the origin (Figure 2). Thus, our new equations are:
- Wx=0
- Wx=1
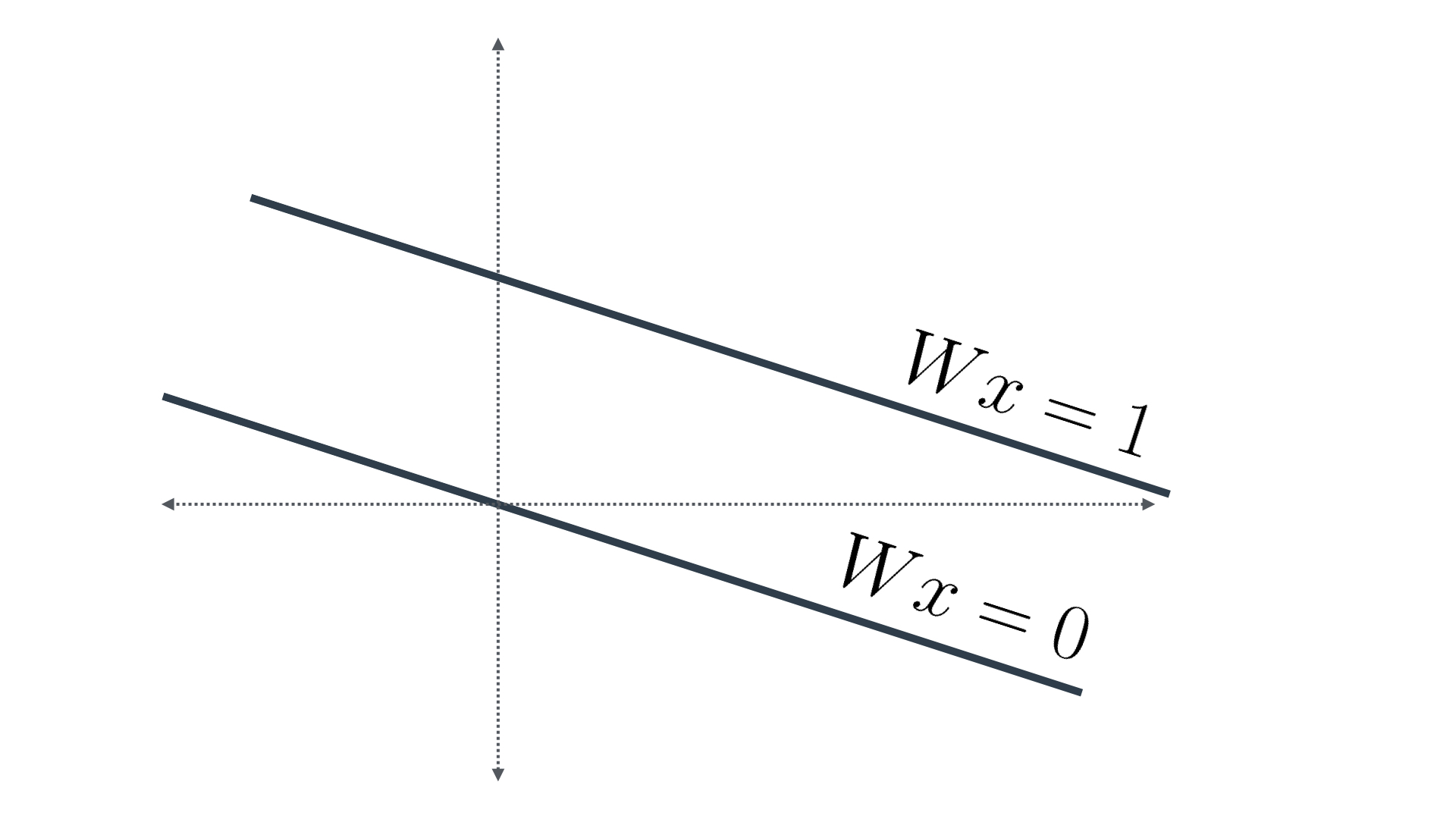
Figure 2
Now, the first line has equation Wx=0, which means it's orthogonal (perpendicular) to the vector W = (w_1, w_2) colored in red (Figure 3).
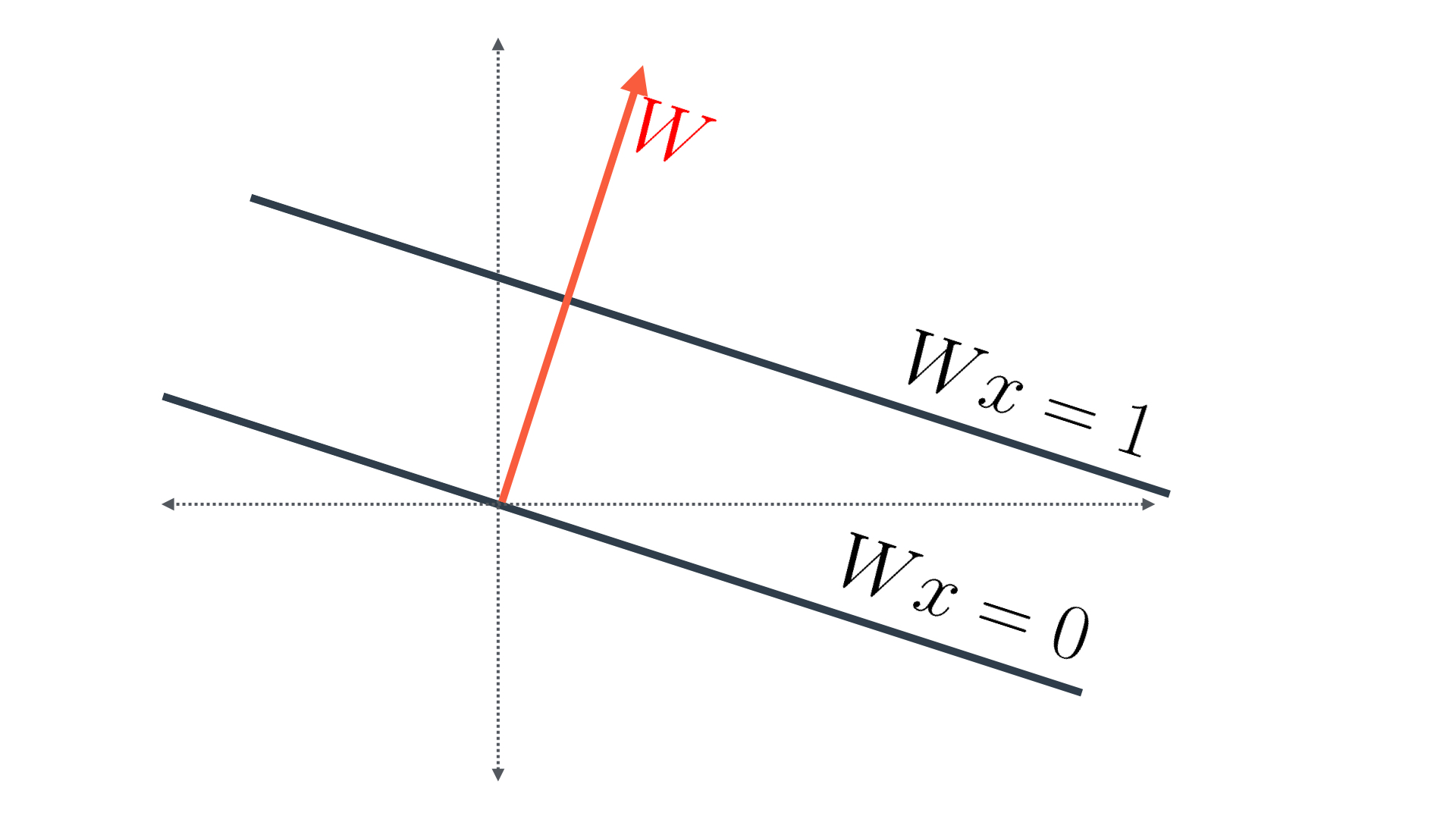
Figure 3
This vector intersects the line of equation Wx=1 at the blue point (Figure 4). Let's say the point has coordinates (p,q). Then, we know two things:
- w_1p + w_2q = 1 (since the point is over the line), and
- (p,q) is a multiple of (w_1, w_2), since the point is over the vector W = (w_1, w_2).
We can solve these two equations as follows: Let (p,q) = k(w_1, w_2) for some k. That turns our first equation into k(w_1^2 + w_2^2) = 1. Therefore, k = \frac{1}{w_1^2+w_2^2} = \frac{1}{|W|^2}. That means, our blue point represents the vector \frac{W}{|W|^2}, as shown in Figure 4.
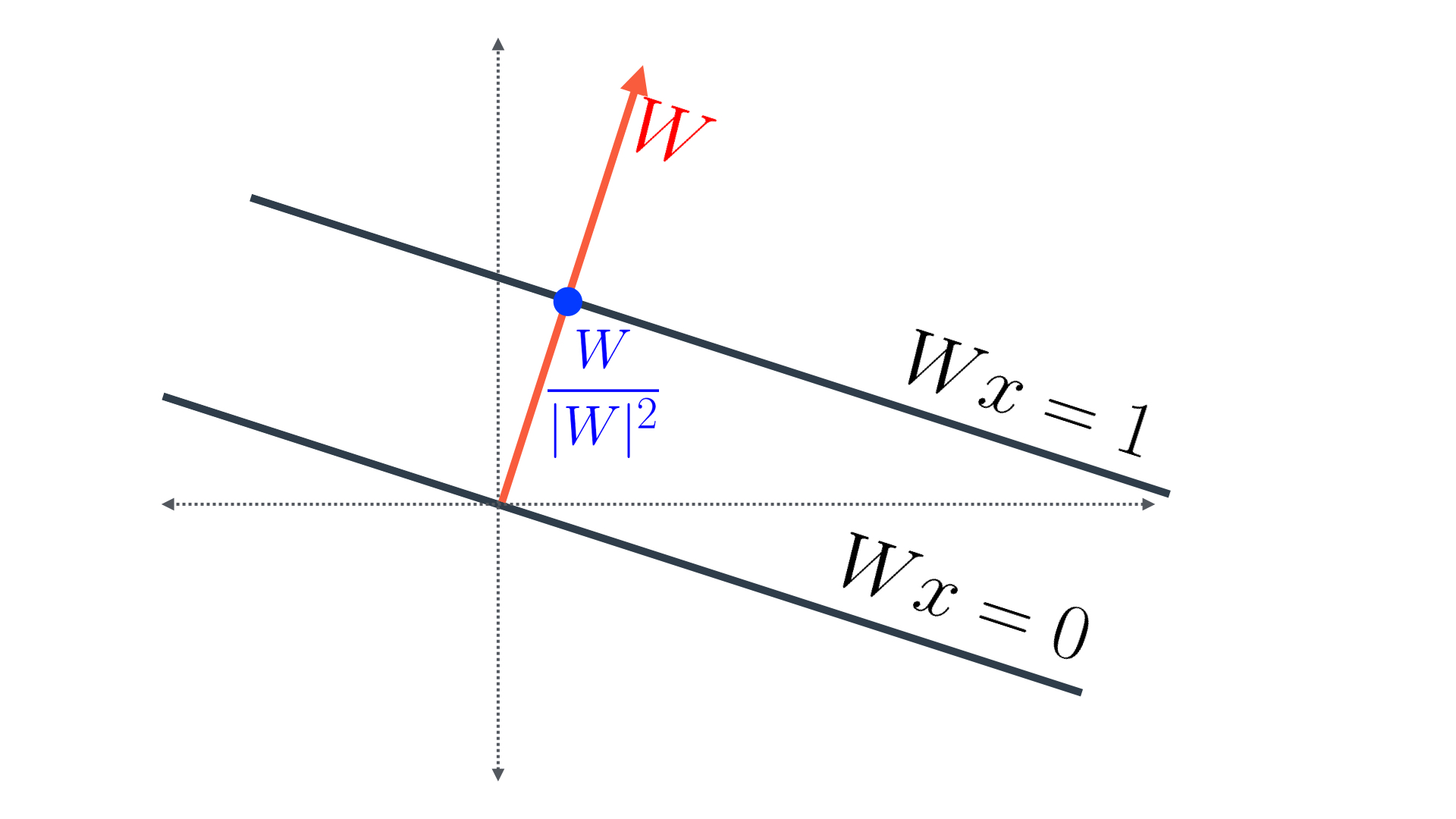
Figure 4
Now, the distance between the two lines, is simply the norm of the blue vector. Since the denominator is a scalar, one can see that the norm of the vector \frac{W}{|W|^2} is precisely \frac{|W|}{|W|^2}, which is the same as \frac{1}{|W|} (Figure 5).
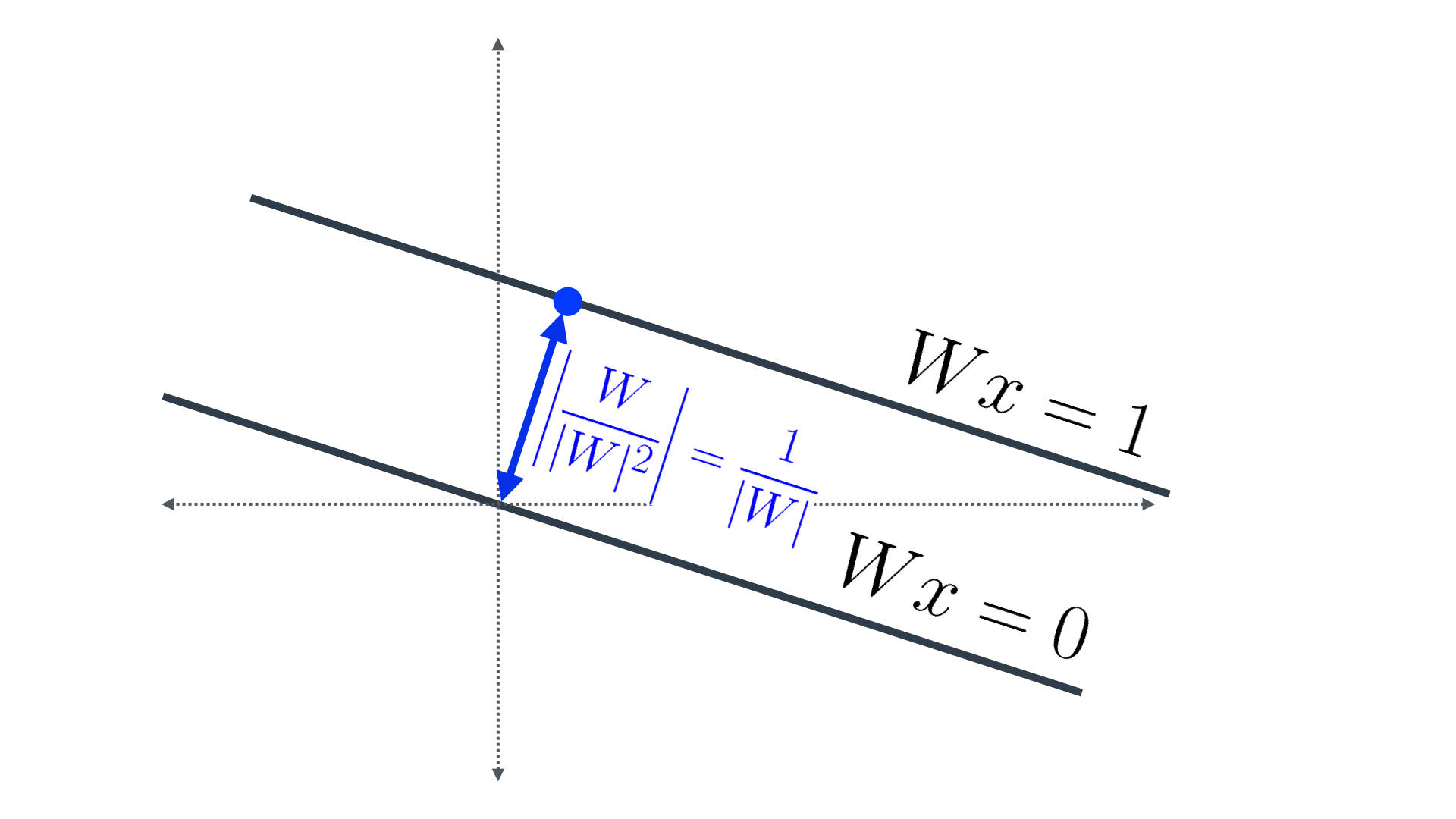
Figure 5
And finally, we remember that the desired distance was the sum of these two distances between the consecutive parallel lines (Figure 6). Since each one of them is \frac{1}{|W|}, then the total distance is \frac{2}{|W|}.
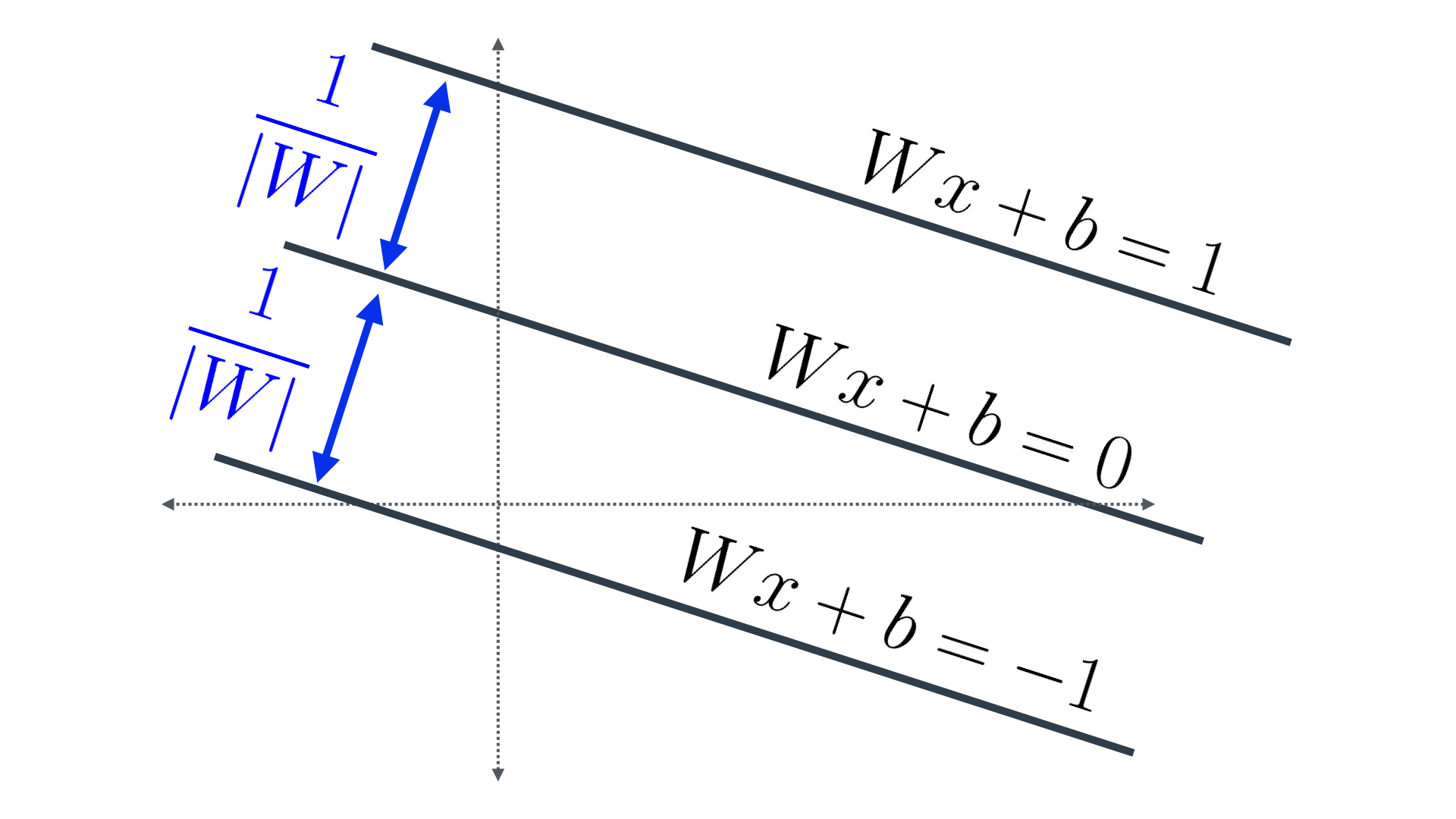
Figure 6